Quick Sort(퀵 정렬)는 분할 정복 접근 방식을 따르는 정렬 알고리즘입니다. 아직 정렬되지 않은 배열을 Pivot(기준 값)을 기준으로 분할하여 작은 값과 큰 값으로 분리한 후, 하위 배열들을 재귀적으로 정렬합니다.
Quick Sort의 정의
Quick Sort(퀵 정렬)는 Divide and Conquer(분할 정복 접근 방식)을 따르는 널리 사용되는 정렬 알고리즘입니다. 이 알고리즘은 배열에서 피벗 요소를 선택하고, 나머지 요소들을 피벗보다 작은지 큰지에 따라 두 개의 하위 배열로 분할합니다. 그런 다음, 하위 배열들은 동일한 과정을 반복하여 재귀적으로 정렬됩니다. 대용량 데이터셋에 효율적이며, 평균 시간 복잡도는 O(n log n)입니다. 하지만 반드시 O(n log n) 이 보장되는 것은 아니고, 최악의 경우에는 시간 복잡도가 O(n^2)가 될 수 있습니다.
분할 정보 접근 방식 (Divide and Conquer)
참고로 Quick Sort 알고리즘을 이해하기 위해서는 Divide and Conquer(분할 정보 접근 방식)로 일컬어지는 문제 해결 방식을 이해해야 하기 때문에 여기에서 간단히 소개하고자 합니다. 분할 정보 접근 방식은 주어진 문제를 더 작은 하위 문제로 분할하고, 각 하위 문제를 재귀적으로 해결한 다음, 이를 다시 결합하여 원래 문제의 해답을 얻는 방법입니다. 여기에서 설명하는 quick sort 뿐만 아니라 사실 binary search 또한 이러한 분할 정보 접근 방식을 이용하고 있다고 보시면 됩니다.
분할 정보 접근 방식은 다음과 같은 단계로 구성됩니다:
- 분할 (Divide): 주어진 문제를 더 작은 하위 문제로 분할합니다. 이 단계에서 문제를 해결하기 쉽고 관리 가능한 크기로 분할합니다.
- 정복 (Conquer): 각 하위 문제를 재귀적으로 해결합니다. 이 단계에서 각 하위 문제의 해답을 얻습니다.
- 결합 (Combine): 각 하위 문제의 해답을 결합하여 원래 문제의 해답을 얻습니다.
분할 정보 접근 방식은 문제를 작은 단위로 분할하여 해결하므로, 복잡한 문제를 해결하는 데 효과적입니다. 퀵 정렬과 같은 알고리즘은 분할 정보 접근 방식을 사용하여 대용량 데이터셋에서 효율적으로 작동합니다. 그러나 최악의 경우에는 성능이 저하될 수 있으므로 이러한 알고리즘을 사용할 때는 주의가 필요합니다.
Quick Sort 코딩 예제
Quick Sort 알고리즘을 Python 코드로 작성해서 보여줍니다.
def quickSort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quickSort(left) + middle + quickSort(right)
# Test the function
arr = [3, 6, 8, 10, 1, 2, 1]
print(quickSort(arr))
quickSort 함수는 입력 배열 arr을 정렬하는 함수입니다. 배열의 길이가 1 이하인 경우에는 그대로 반환하고, 그렇지 않은 경우에는 피벗(pivot) 값과 비교하여 작은 값은 왼쪽 배열, 피벗 값과 동일한 값은 중간 배열, 큰 값은 오른쪽 배열로 분할합니다. 배열의 길이가 1 이하인 경우는 배열 자체가 비어 있거나 혹은 배열을 이루는 요소가 하나일 경우입니다. 즉 이 두 가지 의 경우 모두 정렬할 필요가 없는 배열을 의미합니다. 위에서 설정한 pivot 값이라 함은 배열을 양쪽으로 정렬하여 분할할 수 있는 중심 값이라 생각하시면 되고, 이에 대한 값 지정은 일반적으로 아직 정렬되지 않은 배열의 중앙값으로 지정합니다. 이렇게 분할된 배열들을 각각 재귀적으로 Quick Sort를 호출하여 정렬을 수행하고, 결합하여 최종 정렬된 배열을 반환합니다. 예제에서는 arr에 [3, 6, 8, 10, 1, 2, 1]을 입력하여 Quick Sort를 수행하고, 정렬된 결과인 [1, 1, 2, 3, 6, 8, 10]을 출력하고 있습니다.
Quick Sort 알고리즘 작동 기본 이미지
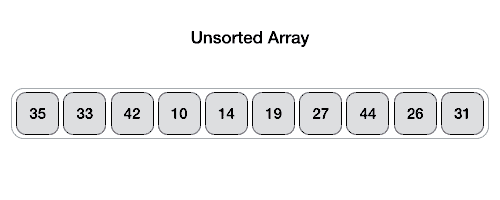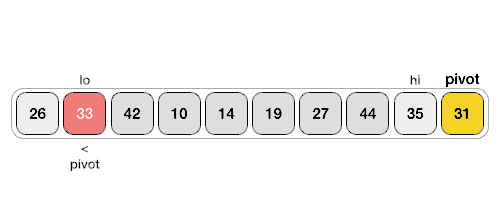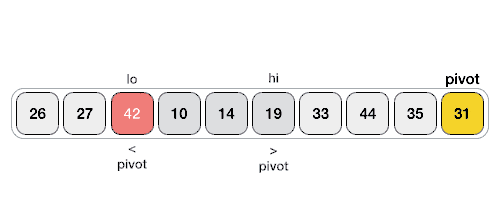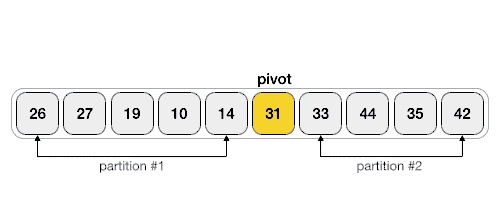
Quick Sort 알고리즘의 장, 단점
장점
- 효율성: Quick Sort는 평균적으로 O(n log n)의 시간 복잡도를 가지며 대용량 데이터셋에서 효율적으로 작동합니다. 또한, 작은 배열이나 부분적으로 정렬된 배열에 대해서도 효율적입니다.
- 제자리 정렬: Quick Sort는 입력 배열 내에서 요소를 교환하여 정렬하므로 추가적인 메모리가 필요하지 않습니다.
- 간결함: Quick Sort 알고리즘은 비교적 직관적인 로직을 가지고 있어 이해하기 쉽고 구현하기도 비교적 간단합니다.
단점
- 최악의 경우 성능 저하: Quick Sort는 최악의 경우에는 O(n^2)의 시간 복잡도를 가질 수 있습니다. 이미 정렬된 배열이나 역순으로 정렬된 배열에서는 성능이 저하될 수 있습니다.
- 불안정한 정렬: Quick Sort는 값이 같은 두 개의 요소를 정렬할 때 순서가 보장되지 않습니다. 따라서 정렬 결과의 순서가 입력 순서와 다를 수 있습니다.
- 피벗 선택의 중요성: Quick Sort의 성능은 선택된 피벗에 크게 의존합니다. 피벗을 항상 최적으로 선택하는 것은 어렵기 때문에 피벗 선택에 따라 성능이 달라질 수 있습니다.
- 최악의 경우 추가적인 메모리 사용: Quick Sort는 재귀적으로 동작하며, 재귀 호출을 위해 추가적인 메모리 스택을 사용합니다. 따라서 최악의 경우 스택 오버플로우가 발생할 수 있습니다.
Quick Sort와 Selection Sort의 장, 단점 비교
Quick Sort
장점: O(n log n)의 평균 시간 복잡도로 대용량 데이터셋에서 효율적입니다. 제자리 정렬이므로 추가적인 메모리가 필요하지 않으며 구현이 간단하고 직관적입니다.
단점: 앞서 언급했듯이 Pivot (분할의 중심이 되는 값) 선택에 따라 시간 복잡도가 O(n^2)가 될 수 있습니다. Recursion 로직을 이용하는 다른 알고리즘과 마찬가지로 재귀적으로 동작하기 때문에 최악의 경우 스택 오버플로우가 발생할 수 있습니다.
Selection Sort
장점: 구현이 간단하고 직관적입니다.
단점: 평균 및 최악의 시간 복잡도는 모두 O(n^2) 이기 때문에 Quick Sort의 경우처럼 대용량 데이터 셋에서는 사용하지 않는 것이 좋습니다. 또한 Quick Sort와 마찬가지로 제자리 정렬이어서 추가적인 메모리가 필요하진 않지만, 교환 연산이 많이 발생하여 비효율적입니다.
(참고로 비교가 되고 있는 Selection Sort에 대해서는 아래의 링크를 참조해 주시기 바랍니다)
캐나다 IT 코딩 Selection Sort
Selection Sort(선택 정렬)는 배열의 정렬되지 않은 부분에서 반복적으로 최소(혹은 최고) 요소를 선택하고 정렬된 부분의 시작에 배치하는 정렬 알고리즘입니다. 이 과정은 전체 배열이 오름차순 (
canadaprogrammer.tistory.com
코딩 테스트 실제 기출문제 - Quick Sort 알고리즘
캐나다 IT 회사에서 출제된 Quick Sort 알고리즘 관련 실제 기출문제를 소개합니다. 영문 자체를 한글로 굳이 번역해서 소개하지 않는 이유는 이런 패턴에 익숙해지셔야 하기 때문입니다. 그리고 Solution을 보시기 전에 반드시 우선 문제 자체를 풀어 보시고 접근하시기 바랍니다.
Question:
Given an array of integers, implement the Quick Sort algorithm to sort the array in ascending order.
Example:
Input: [7, 2, 1, 6, 8, 5] Output:[1, 2, 5, 6, 7, 8]
Solution:
def quickSort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quickSort(left) + middle + quickSort(right)
# Test the function
arr = [7, 2, 1, 6, 8, 5]
sorted_arr = quickSort(arr)
print(sorted_arr)
캐나다 IT 코딩 Recursion
Recursion 알고리즘은 함수가 자기 자신을 호출하여 문제를 해결하는 알고리즘입니다. Base case(기본 사례)에서는 재귀 호출을 멈추는 조건을 설정하고, Recursive case(재귀 사례)에서는 문제를 더 작은
canadaprogrammer.tistory.com
캐나다 IT 코딩 Binary Search
캐나다 IT 개발 구직자에게 코딩 테스트는 필수입니다. 취업, 전직 시에 코딩 테스트를 통과해야 하는 것은 분명하고 또한 개발자로서 준비하고 공부하면서 얻을 수 있는 기회입니다. 이번 글에
canadaprogrammer.tistory.com
'코딩 테스트' 카테고리의 다른 글
| 캐나다 IT 코딩 Breadth-first search (0) | 2023.12.21 |
|---|---|
| 캐나다 IT 코딩 Hash Table (0) | 2023.12.16 |
| 캐나다 IT 코딩 Recursion (0) | 2023.12.09 |
| 캐나다 IT 코딩 Selection Sort (2) | 2023.12.07 |
| 캐나다 IT 코딩 Binary Search (0) | 2023.12.06 |



