너비 우선 탐색(Breadth-first search-BFS)은 그래프 순회 알고리즘으로, 그래프의 모든 정점(Node)을 정확히 한 번만 방문해서 탐색하고, 큐(Queue) 자료 구조를 사용하여 저장하고 필요한 데이터를 추적하는 알고리즘입니다.
Breadth-first search의 정의
Graph, Node 그리고 Edge의 정의
우선 BFS라는 알고리즘을 알기 전에 Graph와 Node 그리고 Node 간의 관계에 대해서 우선 알아보도록 하겠습니다. 의미 자체가 어렵고 이를 구성하는 세부 요소들을 글로 이해하는 것이 애매모호하기 때문에 예를 들도록 하겠습니다. X라고 하는 장소에서 Y 장소에 도달하기 위한 방법으로 우리는 여러 가지 시나리오를 생각할 수 있습니다. 직접적으로 갈 수 있는 방법은 없고 여러 가지 교통편을 이용해야만 도달한다고 가정을 해 봅니다. 아래와 같은 자료구조를 Graph라고 합니다.
- X —> A —> B —> Y
- X —> A —> C —> Y
- X —> B —> D —> Y
- X —> E —> F —> C —> Y
- X —> G —> Y
위와 같은 각각의 세부 요소들을 Node라고 칭하고, Node 가 다른 Node에 의존적이라면 이웃 노드라고 합니다. (X —> G라는 노드 표현은 X 노드가 G 노드에 의존적이라는 의미입니다. 여기에서 화살표 (혹은 간선)는 Edge라고 표현되며 이를 통해 Node 간의 관계를 정의합니다. 화살표가 아닌 일반 선이라면 양방향의 의미이고 위와 같은 화살표는 일방향을 의미합니다.).
BFS 알고리즘의 동작 과정
너비 우선 탐색(Breadth-first search-BFS)은 앞서 설명한 Graph 데이터 구조에서 그 구조를 이루는 Node 들을 정확히 한 번만 방문해서 탐색하고 동시에 큐(Queue) 자료 구조를 사용하여 저장하고 필요한 데이터를 추적하는 알고리즘입니다. 위의 시나리오에서는 이 알고리즘을 통해 X에서 Y에 도달할 수 있는 여러 가지 경우의 수에서 가장 빠른 경로를 찾아낼 수 있습니다. 이렇게 일반적으로 가중치가 없는 그래프에서 두 정점 사이의 최단 경로를 찾는 데 사용되고 있으며 또한 연결 요소 찾기나 사이클 탐지와 같은 다른 그래프 관련 작업에도 사용할 수 있습니다.
Queue의 정의
Queue는 데이터를 선입선출(FIFO) 순서로 저장하는 자료구조입니다. 앞서 언급했듯이 BFS 알고리즘을 이용해서 Node 들을 탐색하게끔 하려면 데이터 형식이 필요한데, 이때 사용되는 것이 Stack과 비슷한 구조의 Queue 라 불리는 데이터 타입입니다. (차이점은 아래에 별도로 언급하겠습니다) 데이터를 삽입하는 enqueue 연산과 데이터를 삭제하는 dequeue 연산을 지원합니다. 큐는 일반적으로 배열이나 연결 리스트로 구현되며, 데이터의 삽입은 큐의 끝(rear)에서 이루어지고, 데이터의 삭제는 큐의 앞(front)에서 이루어집니다. 이러한 특성 때문에 큐는 작업 대기열, 프로세스 관리, 네트워크 패킷 처리 등 다양한 애플리케이션에서 사용됩니다.
Queue와 Stack의 차이
Queue는 선입선출(FIFO, First-In-First-Out) 방식으로 동작합니다. 즉, 가장 먼저 들어온 데이터가 가장 먼저 나가는 구조이고, Stack은 후입선출(LIFO, Last-In-First-Out) 방식으로 동작합니다. 가장 최근에 들어온 데이터가 가장 먼저 나가는 구조입니다. 스택은 push(데이터 삽입)와 pop(데이터 삭제) 연산을 지원하며, 데이터의 삽입과 삭제는 모두 스택의 상단(top)에서 이루어집니다. 대표적인 예로는 함수 호출 스택(Call Stack)이 있습니다. Queue와 Stack은 각각 다른 상황에서 사용됩니다. Queue는 데이터를 순서대로 처리하고자 할 때 사용되며, 처리해야 할 데이터가 많은 경우 유용합니다. 반면에 Stack은 재귀적인 구조나 역순으로 처리해야 할 경우에 사용됩니다.
다음은 Queue와 Stack의 간단 비교입니다:
- Queue: 선입선출(FIFO) 방식, enqueue(삽입)와 dequeue(삭제) 연산을 지원, 대기열이나 버퍼 등에 사용
- Stack: 후입선출(LIFO) 방식, push(삽입)와 pop(삭제) 연산을 지원, 함수 호출 스택 등에 사용
BFS 알고리즘의 실행 단계
- 큐를 초기화하고 출발 Node를 큐에 넣습니다. (Enqueue)
- 출발 정점을 방문한 것으로 표시합니다.
- 큐가 비어 있지 않은 동안 다음을 수행합니다:
- 큐에서 Node를 디큐 합니다. (Dequeue)
- 디큐한 Node를 처리합니다 (예: 값 출력 또는 저장).
- 디큐한 Node의 모든 방문하지 않은 이웃 Node (Neighbor)를 큐에 넣습니다.
- 디큐한 Node을 방문한 것으로 표시합니다.
- 큐가 비어 있을 때까지 단계 3을 반복합니다.
BFS는 출발 정점에서 도달 가능한 모든 정점을 방문하고 처리한 후에야 다음 레벨의 정점으로 넘어가는 것을 보장하는데 바로 이 특성 때문에 BFS는 가중치가 없는 그래프에서 최단 경로를 찾는 데 적합합니다.
BFS 알고리즘은 출발 정점에서 시작하여, 출발 정점과 인접한 정점을 먼저 방문하고 처리합니다. 그다음은 인접한 정점의 인접한 정점을 방문하고 처리하며, 이 과정을 출발 정점에서 도달 가능한 모든 정점을 방문할 때까지 반복합니다. 이러한 방식으로 BFS는 너비 우선으로 그래프를 탐색하게 되는 것입니다. 여기에서 너비 우선의 탐색이라는 의미는 각 노드의 레벨 단위로 검색을 하는 의미로 시작점을 기준으로 레벨을 부여하여 높은 레벨의 노드들을 우선 모두 처리하고 그다음 단계로 하위 레벨로 이동하여 처리를 한다는 개념입니다.
BFS의 시간 복잡도는 O(V + E)이며, 여기서 V는 정점(Node)의 수, E는 그래프의 간선(Edge)의 수입니다.
BFS 코딩 예제
from collections import deque
def bfs(graph, start, end):
# Create a queue for BFS
queue = deque()
# Enqueue the start node
queue.append(start)
# Create a set to keep track of visited nodes
visited = set()
visited.add(start)
# Create a dictionary to keep track of the path
path = {}
path[start] = None
while queue:
# Dequeue a node from the queue
current_node = queue.popleft()
# Check if the current node is the end node
if current_node == end:
break
# Explore the neighbors of the current node
for neighbor in graph[current_node]:
if neighbor not in visited:
# Enqueue the neighbor if it has not been visited
queue.append(neighbor)
# Mark the neighbor as visited
visited.add(neighbor)
# Update the path dictionary
path[neighbor] = current_node
# If there is no path from start to end
if end not in visited:
return "No path found"
# Reconstruct the shortest path
shortest_path = []
current_node = end
while current_node is not None:
shortest_path.append(current_node)
current_node = path[current_node]
shortest_path.reverse()
return shortest_path
# Example graph
graph = {
'A': ['B', 'C'],
'B': ['A', 'D'],
'C': ['A', 'E'],
'D': ['B', 'E', 'F'],
'E': ['C', 'D', 'F'],
'F': ['D', 'E']
}
start_node = 'A'
end_node = 'F'
# Find the shortest path using BFS
shortest_path = bfs(graph, start_node, end_node)
print(shortest_path)이 예제에서는 인접 리스트 표현을 사용하여 그래프를 정의합니다. 위의 bfs 함수는 그래프, 시작 노드 및 종료 노드를 입력으로 받아 시작 노드와 종료 노드 사이의 최단 경로를 찾기 위해 너비 우선 탐색을 수행합니다. 이 함수는 방문할 노드를 추적하기 위해 큐를 사용하고, 방문한 노드를 추적하기 위해 집합을 사용하며, 경로를 추적하기 위해 사전을 사용합니다. 알고리즘은 종료 노드가 찾아지거나 모든 도달 가능한 노드가 방문될 때까지 그래프를 계속 탐색합니다. 경로가 찾아지면 함수는 경로 사전을 사용하여 최단 경로를 재구성합니다.
BFS 작동 기본 이미지
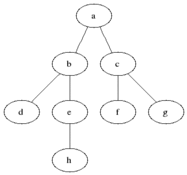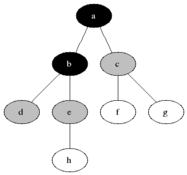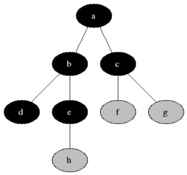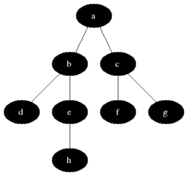
BFS의 장, 단점
BFS 알고리즘의 장점
- 최단 경로 찾기: 가중치가 없는 그래프에서 두 정점 사이의 최단 경로를 찾는 데 사용됩니다.
- 모든 정점 탐색: 그래프의 모든 정점을 탐색하고 방문한 정점을 추적할 수 있습니다.
- 연결 요소 찾기: 그래프의 연결 요소를 찾는 데 사용됩니다.
BFS 알고리즘의 단점
- 메모리 사용량: 큐 자료 구조를 사용하기 때문에 큰 그래프에서는 많은 메모리를 사용할 수 있습니다.
- 시간 복잡도: 시간 복잡도는 O(V + E)로, 정점의 수 V와 간선의 수 E에 비례합니다.
코딩 테스트 실제 기출문제 - BFS 알고리즘
캐나다 IT 회사에서 출제된 BFS 알고리즘 관련 실제 기출문제를 소개합니다. 영문 자체를 한글로 굳이 번역해서 소개하지 않는 이유는 이런 패턴에 익숙해지셔야 하기 때문입니다. 그리고 Solution을 보시기 전에 반드시 우선 문제 자체를 풀어 보시고 접근하시기 바랍니다.
Question:
In this example, we have a maze represented as a 2D grid of characters. The 'S' represents the starting point, 'E' represents the endpoint, and '#' represents walls. Our goal is to find the shortest path from the start to the end by moving only in empty spaces (' '). We use BFS to explore the maze and find the shortest path. Create the function for bfs
Example:
maze = [
['#', '#', '#', '#', '#', '#', '#', '#', '#', '#'],
['#', 'S', '#', ' ', ' ', ' ', ' ', ' ', ' ', '#'],
['#', ' ', '#', '#', '#', '#', '#', '#', ' ', '#'],
['#', ' ', ' ', ' ', ' ', ' ', ' ', '#', ' ', '#'],
['#', '#', '#', '#', '#', '#', ' ', '#', ' ', '#'],
['#', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', '#'],
['#', ' ', '#', '#', '#', '#', '#', '#', '#', '#'],
['#', ' ', ' ', ' ', ' ', ' ', ' ', ' ', 'E', '#'],
['#', '#', '#', '#', '#', '#', '#', '#', '#', '#'],
]
start_node = (1, 1)
end_node = (7, 8)
# Find the shortest path using BFS
shortest_path = bfs(maze, start_node, end_node)
# Print the shortest path
for node in shortest_path:
row, col = node
maze [row][col] = '*'
for row in maze:
print(' '.join(row))
Solution:
from collections import deque
def bfs(maze, start, end):
rows, cols = len(maze), len(maze[0])
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)] # Possible movements: right, down, left, up
# Create a queue for BFS
queue = deque()
# Enqueue the start node
queue.append(start)
# Create a set to keep track of visited nodes
visited = set()
visited.add(start)
# Create a dictionary to keep track of the path
path = {}
path[start] = None
while queue:
# Dequeue a node from the queue
current_node = queue.popleft()
# Check if the current node is the end node
if current_node == end:
break
# Explore the neighbors of the current node
for direction in directions:
new_row = current_node[0] + direction[0]
new_col = current_node[1] + direction[1]
if 0 <= new_row < rows and 0 <= new_col < cols and maze[new_row][new_col] != '#' and (new_row, new_col) not in visited:
# Enqueue the neighbor if it has not been visited
queue.append((new_row, new_col))
# Mark the neighbor as visited
visited.add((new_row, new_col))
# Update the path dictionary
path[(new_row, new_col)] = current_node
# If there is no path from start to end
if end not in visited:
return "No path found"
# Reconstruct the shortest path
shortest_path = []
current_node = end
while current_node is not None:
shortest_path.append(current_node)
current_node = path[current_node]
shortest_path.reverse()
return shortest_path
캐나다 IT 코딩 Selection Sort
Selection Sort(선택 정렬)는 배열의 정렬되지 않은 부분에서 반복적으로 최소(혹은 최고) 요소를 선택하고 정렬된 부분의 시작에 배치하는 정렬 알고리즘입니다. 이 과정은 전체 배열이 오름차순 (
canadaprogrammer.tistory.com
캐나다 IT 코딩 Hash Table
Hash Table은 키와 값으로 데이터를 저장하는 자료구조입니다. 키를 해시 함수를 통해 해시값으로 변환하여 인덱스로 사용하며, 이를 통해 빠른 데이터 접근이 가능합니다. O(1)의 평균 시간 복잡도
canadaprogrammer.tistory.com
'코딩 테스트' 카테고리의 다른 글
| 캐나다 IT 코딩 Dijkstra (0) | 2024.01.06 |
|---|---|
| 캐나다 IT 코딩 Hash Table (0) | 2023.12.16 |
| 캐나다 IT 코딩 Quick Sort (0) | 2023.12.12 |
| 캐나다 IT 코딩 Recursion (0) | 2023.12.09 |
| 캐나다 IT 코딩 Selection Sort (2) | 2023.12.07 |



